Tuning a Machine Learning Model
Regularization
Regularization is a method to balance overfitting and underfitting a model during training. Both overfitting and underfitting are problems that ultimately cause poor predictions on new data.
Overfitting occurs when a machine learning model is tuned to learn the noise in the data rather than the patterns or trends in the data. Models are frequently overfit when there are a small number of training samples relative to the flexibility or complexity of the model. Such a model is considered to have high variance or low bias. A supervised model that is overfit will typically perform well on data the model was trained on but perform poorly on data the model has not seen before.
Underfitting occurs when the machine learning model does not capture variations in the data – where the variations in data are not caused by noise. Such a model is considered to have high bias, or low variance. A supervised model that is underfit will typically perform poorly on both data the model was trained on, and on data the model has not seen before. Examples of overfitting, underfitting, and a good balanced model, are shown in the following figure.
Figure 14 Regularization helps to balance variance and bias during model training.
Regularization is a technique to adjust how closely a model is trained to fit historical data. One way to apply regularization is by adding a parameter that penalizes the loss function when the tuned model is overfit. This allows use of regularization as a parameter that affects how closely the model is trained to fit historical data. More regularization prevents overfitting, while less regularization prevents underfitting. Balancing the regularization parameter helps find a good tradeoff between bias and variance.
Regularization is incorporated into model training by adding a regularization term to the loss function, as shown by the loss function example that follows. This regularization term can be understood as penalizing the complexity of the model.
Recall that we defined the machine learning model to predict outcomes Yem> based on input features X as Y = f(X).
And we defined a loss function J(θ) for model training as the mean squared error (MSE):
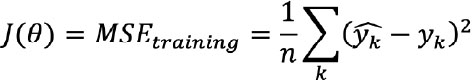
One type of regularization (L2 regularization) that can be applied to such a loss function with regularization parameter λ is:
Where yk represents a model prediction, yk represents an actual value, there are n data points, and m features.