- AI Software
- C3 AI Applications
- C3 AI Applications Overview
- C3 AI Anti-Money Laundering
- C3 AI Cash Management
- C3 AI Contested Logistics
- C3 AI CRM
- C3 AI Decision Advantage
- C3 AI Demand Forecasting
- C3 AI Energy Management
- C3 AI ESG
- C3 AI Health
- C3 AI Intelligence Analysis
- C3 AI Inventory Optimization
- C3 AI Process Optimization
- C3 AI Production Schedule Optimization
- C3 AI Property Appraisal
- C3 AI Readiness
- C3 AI Reliability
- C3 AI Smart Lending
- C3 AI Supply Network Risk – bak
- C3 AI Turnaround Optimization
- C3 Generative AI Constituent Services
- C3 Law Enforcement
- C3 Agentic AI Platform
- C3 Generative AI
- Get Started with a C3 AI Pilot
- Industries
- Customers
- Events
- Resources
- Generative AI for Business
- Generative AI for Business
- C3 Generative AI: How Is It Unique?
- Reimagining the Enterprise with AI
- What To Consider When Using Generative AI
- Why Generative AI Is ‘Like the Internet Circa 1996’
- Can the Generative AI Hallucination Problem be Overcome?
- Transforming Healthcare Operations with Generative AI
- Data Avalanche to Strategic Advantage: Generative AI in Supply Chains
- Supply Chains for a Dangerous World: ‘Flexible, Resilient, Powered by AI’
- LLMs Pose Major Security Risks, Serving As ‘Attack Vectors’
- What Is Enterprise AI?
- Machine Learning
- Introduction
- What is Machine Learning?
- Tuning a Machine Learning Model
- Evaluating Model Performance
- Runtimes and Compute Requirements
- Selecting the Right AI/ML Problems
- Best Practices in Prototyping
- Best Practices in Ongoing Operations
- Building a Strong Team
- About the Author
- References
- Download eBook
- All Resources
- Publications
- Customer Viewpoints
- Blog
- Glossary
- Developer Portal
- Generative AI for Business
- News
- Company
- Contact Us
Glossary
- Artificial Intelligence
- AI Agents
- AI in Finance
- AI in Manufacturing
- Anomaly Detection
- Anti-Money Laundering
- Asset Performance Management
- Asset Reliability
- Demand Forecasting
- Digital Disruption
- Digital Transformation
- Digital Twin
- Elastic Cloud Computing
- Energy Management
- Enterprise AI
- Enterprise AI Platform
- Ethical AI
- Inventory Planning
- IoT Platform
- Know Your Customer (KYC)
- Machine Vision (Computer Vision)
- Model-Driven Architecture
- Multi-Cloud
- No Code
- Predictive Analytics
- Predictive Maintenance
- Process Optimization
- Production Scheduling
- Stochastic Optimization
- Supply Chain Management
- Type System
- Data Unification & Management
- Machine Learning (A to L)
- Artificial General Intelligence
- Bias
- Canonical Schema
- Canonical Transform
- Classification
- Classifier
- Classifier Performance
- Clustering
- Coefficient of Discrimination, R-Squared (R2)
- Convolutional Neural Network (CNN)
- Correlation
- Data Cleansing
- Data Labels
- Data Lineage
- Deep Learning
- Dimensionality Reduction
- Explainable AI
- F1 Score
- False Positive Rate
- Feature Engineering
- Feedback Loop
- Field Validation
- Gaussian Mixture Model (GMM)
- Generalized Linear Models
- Gradient-Boosted Decision Trees (GBDT)
- Features
- Ground Truth
- Holdout Data
- Hyperparameters
- Information Leakage
- LIME: Local Interpretable Model-Agnostic Explanations
- Linear Regression
- Loss Function
- Low-Dimensional Representation
- Machine Learning (M to Z)
- Mean Absolute Error
- Mean Absolute Percent Error
- Machine Learning Pipeline
- Model Drift
- Model Prototyping
- Model Training
- Model Validation
- Normalization
- Overfitting
- Precision
- Problem Tractability
- Random Forest
- Recall
- Receiver Operating Characteristic (ROC) Curve
- Regression Performance
- Regularization
- Reinforcement Learning
- Reporting Bias
- Ridge Regression
- Root Mean Square Error (RMSE)
- Selection Bias
- Shapley Values
- Supervised Machine Learning
- Tree-Based Models
- Underfitting
- Unsupervised Machine Learning
- XGBoost
Ridge Regression
What is Ridge Regression?
Ridge regression, or Tikhonov regularization, is an extension of ordinary least squares (linear) regression with an additional l2-penalty term (or ridge constraint) to regularize the regression coefficients. Machine learning models that leverage ridge regression identify the optimal set of regression coefficients as follows
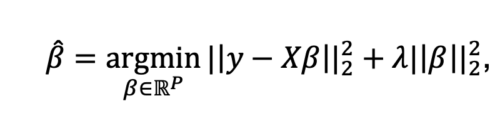
where ![]() is the dependent/target variable whose value the model is trying to predict using N samples of training data,
is the dependent/target variable whose value the model is trying to predict using N samples of training data, ![]() , and P features. The “shrinkage parameter” or “regularization coefficient”, λ, controls the l2 penalty term on the regression coefficients,
, and P features. The “shrinkage parameter” or “regularization coefficient”, λ, controls the l2 penalty term on the regression coefficients, ![]() . Increasing λ forces the regression coefficients in the AI model to become smaller. If λ = 0, the formulation is equivalent to ordinary least squares regression.
. Increasing λ forces the regression coefficients in the AI model to become smaller. If λ = 0, the formulation is equivalent to ordinary least squares regression.
Why is Ridge Regression Important?
Ridge regression adds the l2-penalty term to ensure that the linear regression coefficients do not explode (or become very large). It reduces variance, producing more consistent results on unseen datasets. It also helps deal with multicollinearity, which happens when the P features in X are linearly dependent.
How C3 AI Helps Organizations Use Ridge Regression
Ridge regression is supported as a machine learning technique in the C3 AI Platform. It is infrequently used in practice because data scientists favor more generally applicable, non-linear regression techniques, such as random forests, which also serve to reduce variance in unseen datasets. However, it works well when there is a strong linear relationship between the target variable and the features. It has been used in a C3 AI Reliability proof of technology for a customer that wanted to predict shell temperatures in industrial heat exchangers using fouling factors as features.



